Introduction

Parkinson's disease is a progressive nervous system disorder affecting movement, often starting with subtle tremors in one hand. This study analyzes the Parkinson's Telemonitoring dataset, predicting total UPDRS scores. It includes biomedical voice data from 42 early-stage Parkinson's patients using a remote monitoring device over six months. The dataset is complete, containing subject info, time intervals, UPDRS scores, and 16 voice measures. Each row is a voice recording. The data is in ASCII CSV format. The "test time" feature indicates when measurements were taken. Total and motor UPDRS scores were measured daily, while other features were measured multiple times. This paper focuses on predicting total UPDRS using other features to reduce costs. The study uses linear least-squares, ridge regression, Adam optimizer, and conjugate gradient methods, with weight plots, error analysis, and comparisons between these algorithms as the main contributions.

Pre-processing

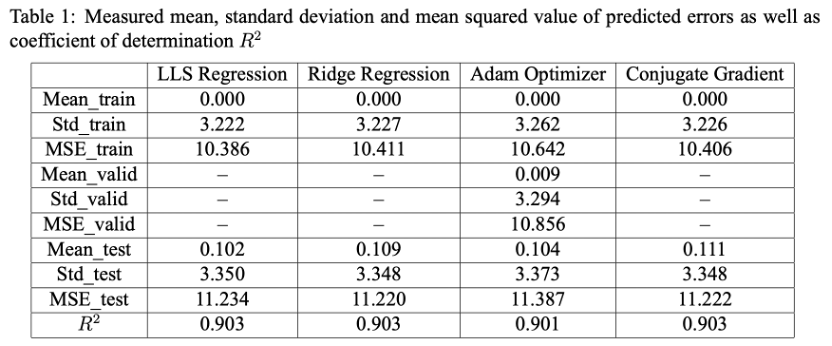
Firstly we visualize the covariance matrix of all the features, as is shown in Figure 1. We can see that it is symmetric and the diagonal elements are much larger than other elements. Since we would like to give a result without knowing which one the patient is and when the test time is, we drop the unwanted features ’subject#’ and ’test_time’ from the data. We also randomly shuffle the rows of the original data to avoid the fact that the training dataset only contains the first parts of the patients. We split the first 50% of the shuffled data as a training set, the subsequent 25% as the validation set, and the remaining 25% as the test set. Meanwhile, in order to avoid numerical problems, data normalization is performed so that each feature has mean zero and variance 1. The mean and standard deviation of the training dataset are evaluated to normalize the three data frames.

Experiment results on different methods

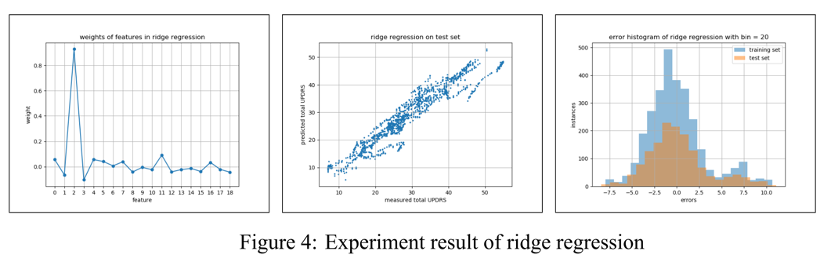
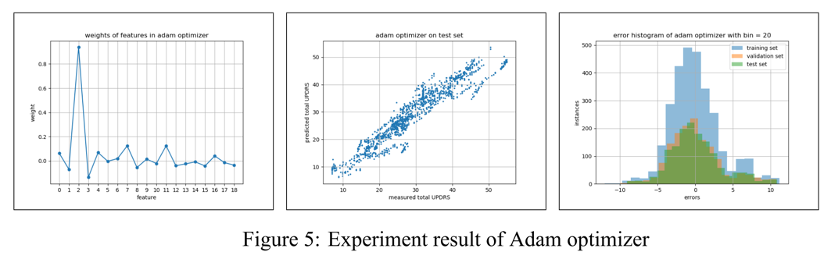
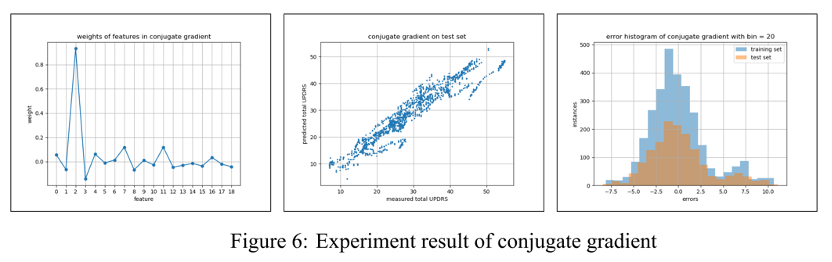
Conclusion

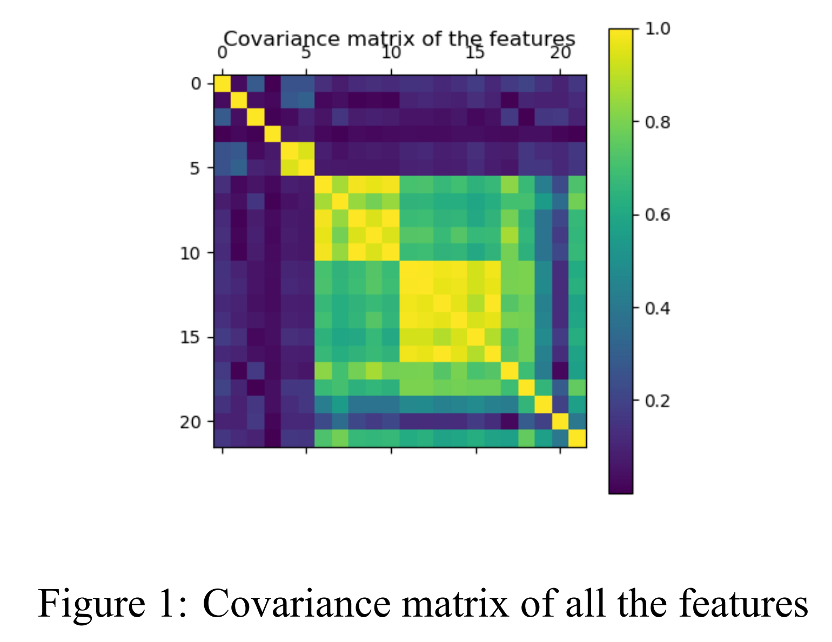
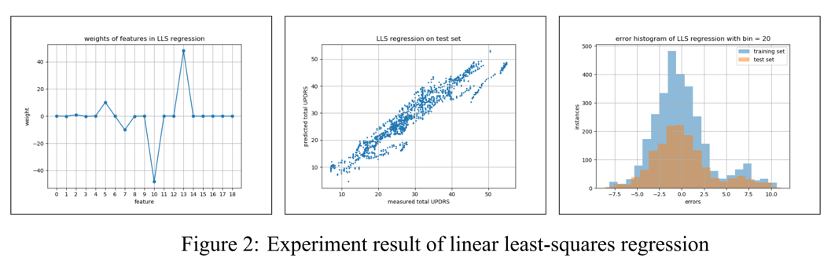
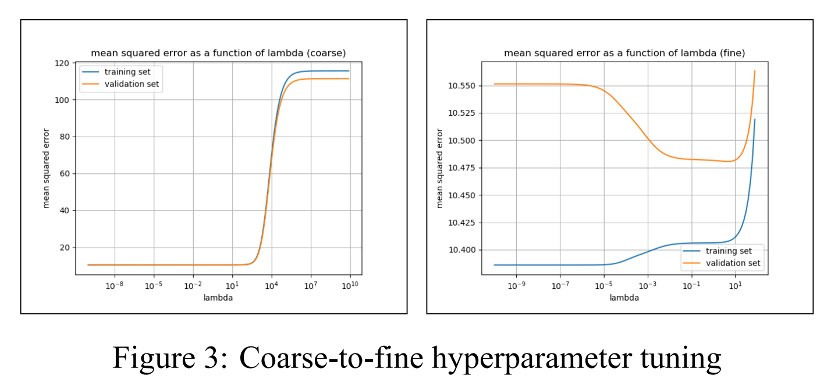
From Figure 2 4 5 6 and Table 1 we can compare the results of the above four algorithms intuitively. Although LLS regression has the smallest mean squared error on the training set, it performs worse than ridge regression and conjugate gradient due to overfitting. Ridge regression achieved a small- est mean squared error with 11.220. The coefficients of determination R2 of LLS regression, ridge regression, and conjugate gradient methods on the test set are all 0.903, which means that 90.3% of the test data could be explained by respective algorithms, while the R2 of Adam optimizer is 0.901.

In our experiment, the Adam optimizer has a maximum mean squared error and has many more iterative steps than conjugate gradient methods. This is because it is tricky to tune so many hyperparameters in the Adam optimizer compared with other algorithms.