MoleSymmetry: Enhancing Melanoma Diagnosis with Advanced Border and Asymmetry Algorithms
Introduction
Melanoma is a type of skin cancer that can spread to other organs in the body. The doctor usually considers 5 features to diagnose melanoma. The 5 so-called "ABCDE" features are A-asymmetry, B- border, C - color, D - diameter, E - evolution. In this report, we focus on borders and asymmetry. We design algorithms to extract these two features to help doctors diagnose melanoma. We evaluate the ratio between the perimeter of the mole and the perimeter of the corresponding circle: the higher this value the more indented the border and the more dangerous the mole. We also invent a way to measure the asymmetry in moles based on that a mole that is an ellipse is symmetric.
Our main contributions to this report are:
1. Design an algorithm to detect the contour of moles.
2. Design an algorithm to evaluate the asymmetry of moles.
1. Design an algorithm to detect the contour of moles.
Dataset
The dataset in this experiment consists of three classes: low risk, medium risk and melanoma case. There are 13, 16 and 27 images in each class respectively. All the moles are roughly in the center of images.
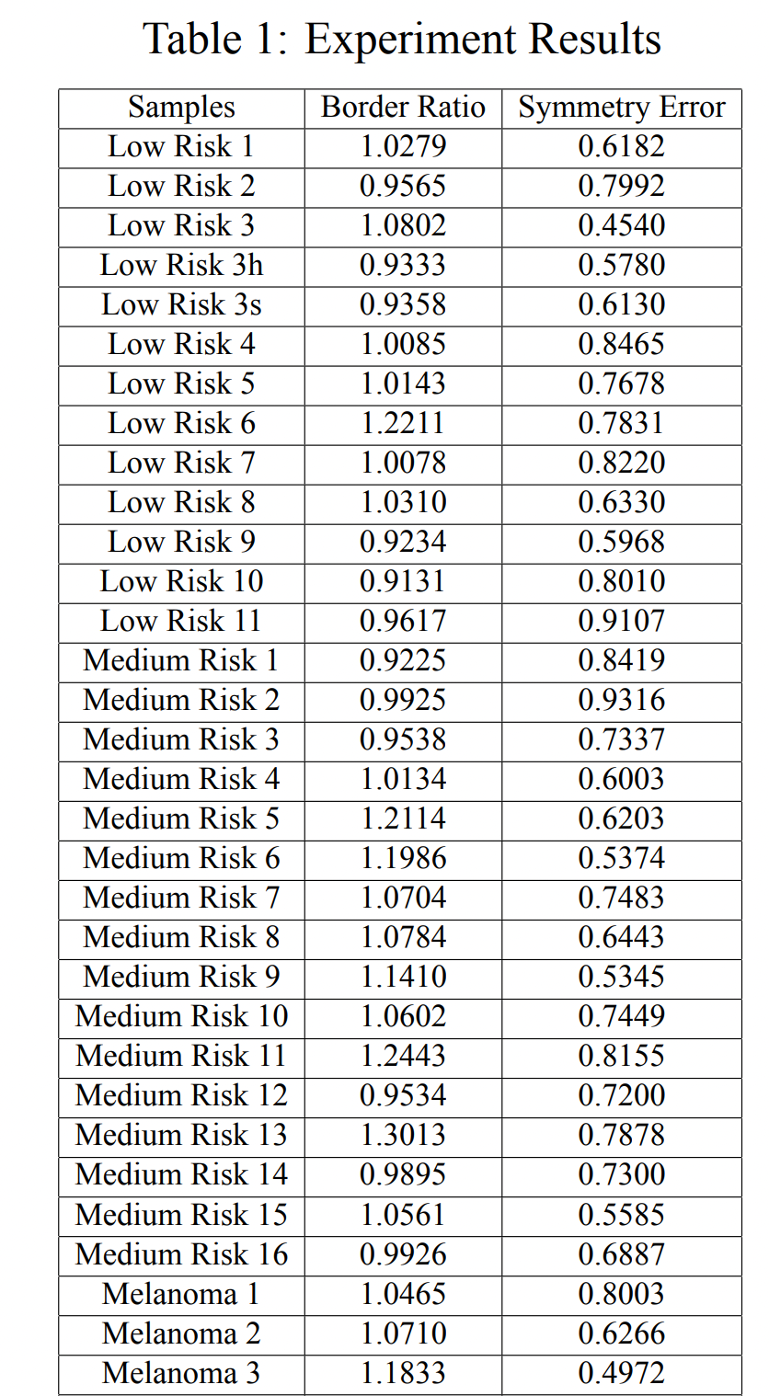
Contour Detection
The contour detection algorithm designed by us can be formulated as follows:
1. Select the region of interest(ROI) which contains the mole.
2. Use K-Means algorithm to cluster the pixels according to the pixel values and choose the cluster with the darkest values to mole.
3. Filter the region of interest to discard the outliers which don’t belong to mole.
4. Find the first and last pixel of the mole in each row and in each column as the contour of the mole.
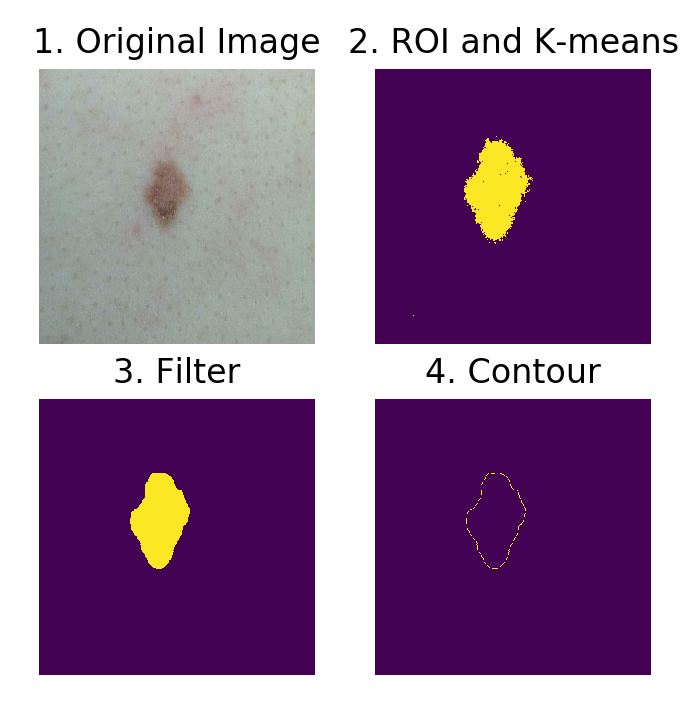
Symmetry Evaluation
The symmetry evaluation algorithm can be formulated as follows:
1. Rotate the mole to align its major axis with x-axis horizontally and its minor axis with y-axis vertically.
2. Divide the mole along x-axis into M portions, for each portion, calculate the difference between top part and bottom part.
3. Divide the mole along y-axis into N portions, for each portion, calculate the difference between left part and right part.
4. Calculate the sum over above differences as the error of symmetry.
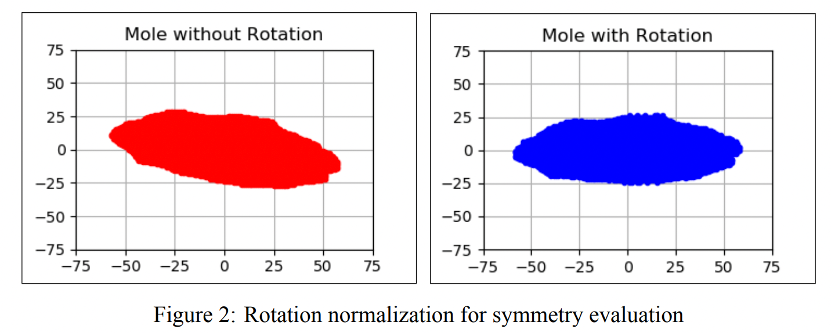
The error of symmetry e is therefore defined as:
where M and N is the number of portions along x-axis and y-axis respectively. For a symmetric object the error e is equal to zero.
Conclusion
The experiment results as well as the statistical values are shown in Table 1. We can find that when the mole becomes serious, the border ratio becomes larger. For the symmetry error, the melanoma case has the maximum value, but the low-risk case has a slightly larger value than the medium-risk case. In this report, we design algorithms to detect the contour of moles and evaluate the asymmetry of moles. We also evaluate the mole dataset using designed algorithms and give the results of the experiment, which show the effectiveness of the proposed algorithms.